Correction - Interrogation A
Exercice 1
1
Coordonnées : \(O (0;0)\), de \(I (1;0)\) et \(J (0;1)\)
2
\(C (-2;1)\), \(D (2;-2)\) 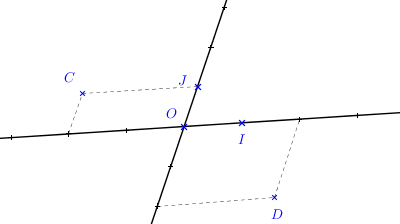
Exercice 2
$$(x_M = \frac{x_A + x_B}{2}; y_M = \frac{y_A + y_B}{2})$$
Exercice 3
1
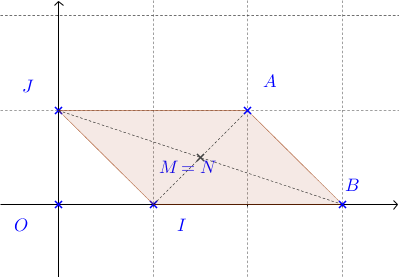 \(A (2;1)\), \(B (3;0)\).
\(A (2;1)\), \(B (3;0)\).
 \(A (2;1)\), \(B (3;0)\).
\(A (2;1)\), \(B (3;0)\).
2
\(M\) est le milieu de \([JB]\)
\[
\begin{aligned}
x_M & = \frac{x_J + x_B}{2} =\frac{0+3}{2} = 1,5 \\
y_M & = \frac{y_J + y_B}{2} =\frac{1+0}{2} = 0,5
\end{aligned}
\]
donc \(M (1,5;0,5)\)
3
\(N\) est le milieu de \([IA]\)
\[
\begin{aligned}
x_N & = \frac{x_I + x_A}{2} =\frac{1+2}{2} = 1,5 \\
y_N & = \frac{y_I + y_A}{2} =\frac{0+1}{2} = 0,5
\end{aligned}
\]
donc \(N (1,5;0,5)\)
4
Le quadrilatère \(JABI\) est un parallélogramme car les diagonales \([JB]\) et \([IA]\) se coupent en leur milieu (les points \(M\) et \(N\) sont confondus d'après les questions précédentes).
Correction - Interrogation B
Exercice 1
1
Coordonnées : \(O (0;0)\), de \(I (1;0)\) et \(J (0;1)\)
2
\(M (-2;-1)\), \(N (1;-2)\) 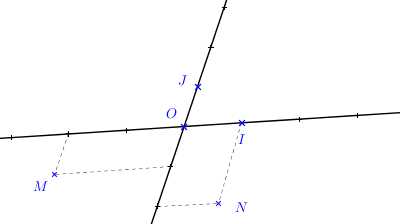
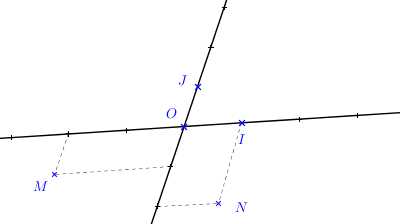
Exercice 2
$$(x_M = \frac{x_A + x_B}{2}; y_M = \frac{y_A + y_B}{2})$$
Exercice 3
1
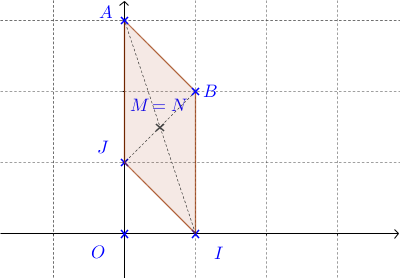 \(A (0;3)\), \(B (1;2)\).
\(A (0;3)\), \(B (1;2)\).
 \(A (0;3)\), \(B (1;2)\).
\(A (0;3)\), \(B (1;2)\).
2
\(M\) est le milieu de \([JB]\)
\[
\begin{aligned}
x_M & = \frac{x_J + x_B}{2} =\frac{0+1}{2} = 0,5 \\
y_M & = \frac{y_J + y_B}{2} =\frac{1+2}{2} = 1,5
\end{aligned}
\]
donc \(M (0,5;1,5)\)
3
\(N\) est le milieu de \([IA]\)
\[
\begin{aligned}
x_N & = \frac{x_I + x_A}{2} =\frac{1+0}{2} = 0,5 \\
y_N & = \frac{y_I + y_A}{2} =\frac{0+3}{2} = 1,5
\end{aligned}
\]
donc \(N (0,5;1,5)\)
4
Le quadrilatère \(JABI\) est un parallélogramme car les diagonales \([JB]\) et \([IA]\) se coupent en leur milieu (les points \(M\) et \(N\) sont confondus d'après les questions précédentes).